交流电路(3):功率计算
功率是电力、电子和通信系统中最重要的量,因涉及从一个点到另一个点的功率传输。 直流电中功率是电压与电流积,那么交流电功率如何计算?

瞬时功率和平均功率
1、瞬时功率(Instantaneous aPower)
元件的瞬时功率 $p(t)$ 是元件两端的瞬时电压 $v(t)$ 与通过它的瞬时电流 $i(t)$ 的乘积:
$$p(t) = v(t)i(t)$$
设电路两端的电压和电流为:
$$v(t) = V_m \cos(\omega t + \theta_v)$$
$$i(t) = I_m \cos(\omega t + \theta_i)$$
其中 $V_m$ 和 $I_m$ 是振幅(或峰值),$θ_v$ 和 $θ_i$ 分别是电压和电流的相位角。 电路吸收的瞬时功率为:
$$p(t) = v(t)i(t) = V_m I_m \cos(\omega t + \theta_v) \cos(\omega t + \theta_i)$$
我们应用三角恒等式并得到瞬时功率$p(t)$:
$$p(t) = \frac{1}{2}V_mI_m \cos(\theta_v - \theta_i) + \frac{1}{2}V_mI_m\cos(2\omega t + \theta_v + \theta_i)$$
瞬时功率随时间变化,因此很难测量。实际应用中平均功率更方便,而且功率表测量的也是平均功率。
2、平均功率(Average Power)
平均功率,以瓦特为单位,是一个周期内瞬时功率的平均值。
$$P = \frac{1}{T} \int _0^T p(t)\delta t$$
代入瞬时功率$p(t)$进一步求解得到:
$$P = \frac{1}{2} V_m I_m \cos(\theta_v - \theta_i)$$
请注意瞬时功率 $p(t)$ 是随时间变化的,而 平均功率$P$ 不依赖于时间。 要计算瞬时功率,我们必须在时域中计算 $v(t)$ 和 $i(t)$的积。 若是计算平均功率,我们既可以计算电压和电流在时域的积分,也可以通过相量域的乘积。
$P$ 也可以通过相量 $V$ 和 $I$ 来计算:
$$P = \frac{1}{2} Re[\textbf{VI}^*] = \frac{1}{2} V_m I_m \cos(\theta_v - \theta_i)$$
有效值或均方根值(Effective or RMS Value)
交流电流的有效值是指向电阻器提供相同的平均功率的直流电流值;交流电压的有效值是指向电阻器提供相同的平均功率的直流电压值。如下图(a)是交流电路,下图(b)是换成有效值电流、电压的直流电路。
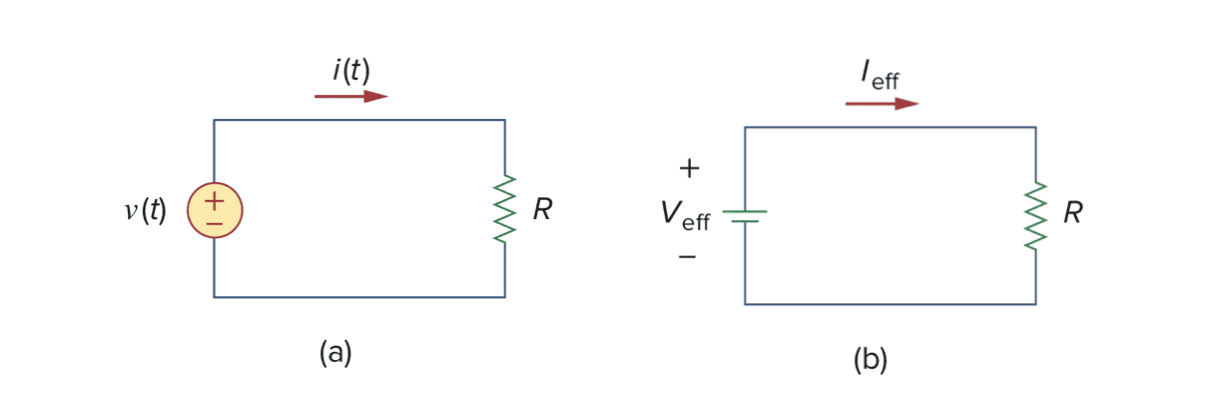
图(a)与图(b)的平均功率相等,即:
$$\frac{1}{T} \int_0^T i^2 R \delta t = I_{eff}^2 R$$
由此得到$I_{eff}$:
$$I_{eff} = \sqrt{\frac{1}{T}\int_0^t i^2 \delta t}$$
右边的即为均方根值(Root mean square value),即:
$$I_{eff} = I _{rms}$$
以同样的思路可以得到交流电压的有效值/圴方根值
$$V_{eff} = \sqrt{\frac{1}{T}\int_0^t v^2 \delta t} = V_{rms}$$
对于正弦曲线 $i(t) = I_m \cos (ωt)$,有效值或 $rms$ 值为:
$$I_{rms} = \sqrt{\frac{1}{T}\int_0^t I_m^2 \cos^2 {\omega t} \delta t} = \frac{I_m}{\sqrt{2}}$$
类似地,对于 $v(t)=V_m \cos \omega t$:
$$V_{rms}=\frac{V_m}{\sqrt{2}}$$
有了均方根值的概念,平均功率可以用 $rms$ 值表示:
$$P = \frac{1}{2} V_m I_m \cos(\theta_v - \theta_i) = V_{rms}I_{rms}\cos(\theta_v - \theta_i)$$
电力行业根据其均方根值而不是峰值指定相量幅度。 比如家家户户都有的110V就是电力公司的电压有效值。 在功率分析中,用均方根值表示电压和电流很方便。 此外,模拟电压表和电流表设计用于分别直接读取电压和电流的均方根值。



