直流电路(1):理论基础
那些贯穿于初中物理、高中物理甚至大学物理的欧姆定律、基尔霍夫定律,可以说是电力、电机、控制、电子、通信和仪器仪表等电气工程的基础,因此有必要将这两个概念理解透彻。本篇文章将深入浅出地讲解这些概念。

基本概念
直流电路基础涉及电荷(Charge)、电流(Current)、电压(Voltage)、能量(Energy)、功率(Power)等概念,务必要理解这些概念的定义及相互之间的关系,不懂的完全可以问AI。
1、电荷
电荷是物质的一种物理性质,分为正电荷与负电荷。负电荷由电子携带,正电荷由原子核中的质子携带。如果电子多于质子,物质就会带负电;如果电子少于质子,物质就会带正电;如果电子与质子数量相等,物质就会呈电中性。
电荷量用q来表示,单位为库伦(C)。电荷为基本电荷(Elementary Electrical Charge)$e$的整数倍(电荷的量子性),基本电荷$e$的量为$1.602× 10^-19$库仑。质子带有电荷量$e$;电子带有电荷量$-e$。
2、电流
电流为电荷的变化率,单位为安培(A),用数学公式表示为:
$$i = \frac{\delta q}{\delta t}$$
$$1 A = 1 \frac{C}{s}$$
根据电流的定义,知道电流可以通过积分来算电荷转移量:
$$q = \int_{t_0}^{t} i \delta t$$
3、电压
电压又称为电势差,是将单位电荷(Unit Charge)从参考点(Reference Point)到另外一点(Another Point)所需要的能量,用$v_{ab}$表示。
$$v_{ab} = \frac{\delta w}{\delta q}$$
$v_{ab}$代表了a点相对于b点的电势,$v_{ab} = - v_{ba}$。
通常用(-)表示参考点,(+)表示另外一点。下图两种方式表示$v_{ab}$是等效的。
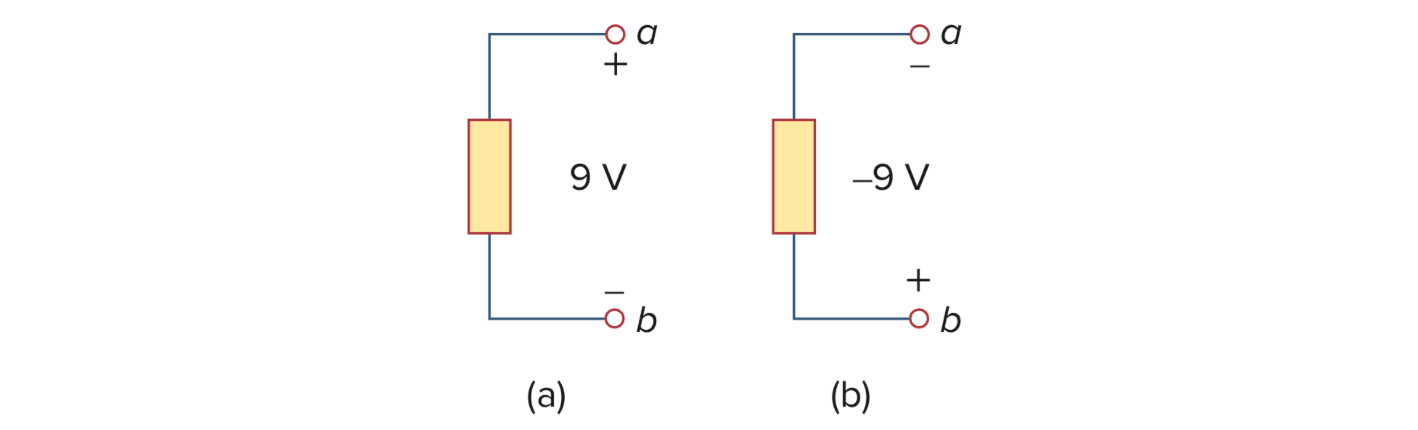
其中能量的单位是焦耳(J),由定义可得到:
$$1 V = 1 \frac{j}{C}$$
4、能量与功率
功率是消耗或吸收能量的时间速率,以瓦特 (W) 为单位测量。功率p的定义为:
$$p = \frac{\delta w}{\delta t}$$
可推导功率与电压、电流的关系:
$$p = \frac{\delta w}{\delta t} = \frac{\delta w}{\delta q} \cdot \frac{\delta q}{\delta t} = vi$$
如果功率为正,表示能量被元件吸收;如果功率为负,表示能量由元件提供。如果电流通过元件的正极,功率为正;如果电流先通过元件的负极,功率为负。功率的正负遵循被动符号约定(Passive sign convention)。
以下是功率为正的案例,电流均通过元件的正极。
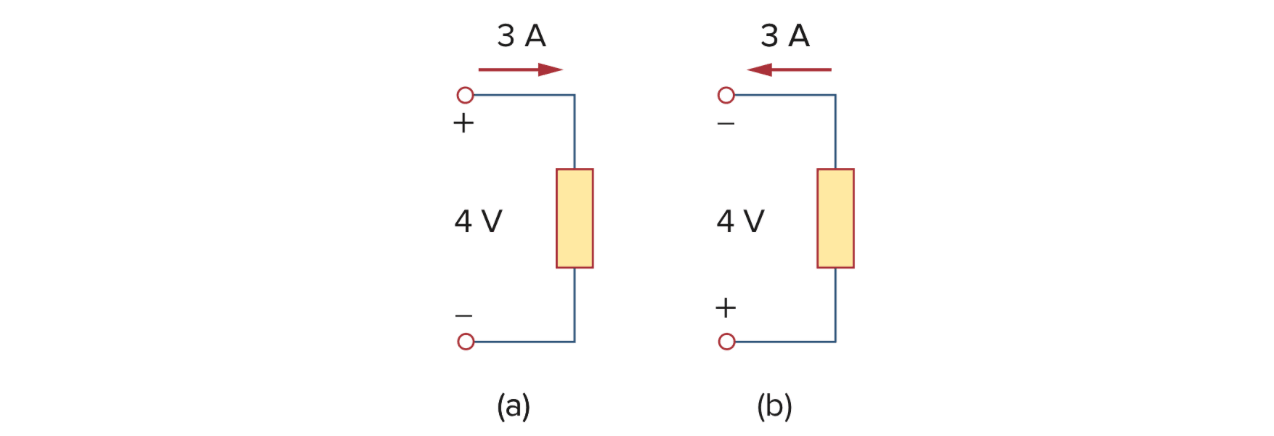
以下是功率为负的案例,电流均通过元件的负极
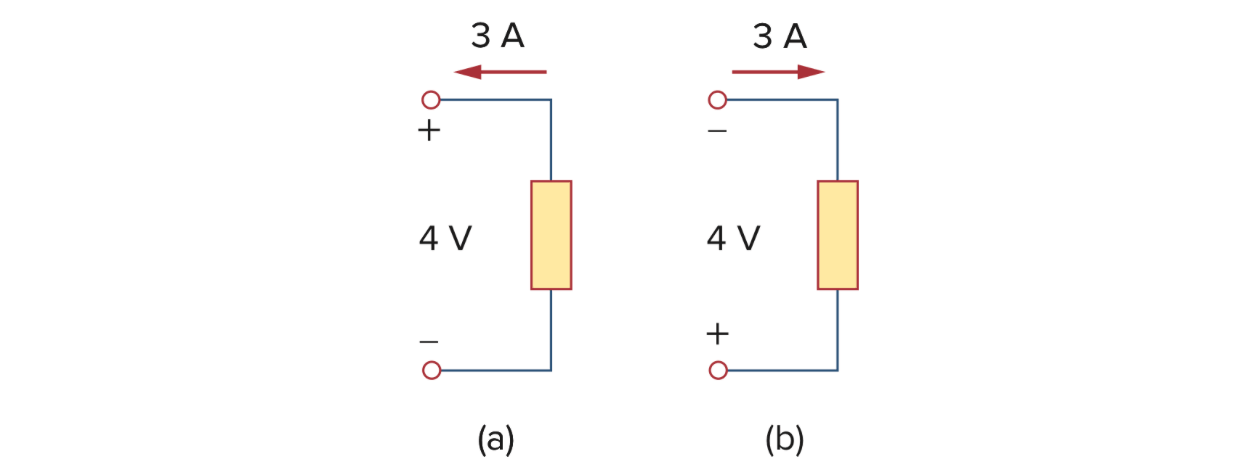
基本定律
如何确定电路中电流、电压与功率之间的关系?我们需要了解电路的基本定律:欧姆定律和基尔霍夫定律。这两个定律构成了电路分析的基础。
1、欧姆定律(Ohm's Law)
材料通常具有抵抗电荷流动的特征行为。 这种抵抗电流的物理特性被称为电阻,用符号 $R$ 表示,单位为$\Omega$。欧姆定律确定了电阻,电流与电压之间的关系,即:
$$R = \frac{v}{i}$$
$$1\Omega = 1 \frac{V}{A}$$
应用欧姆定律之前,我们必须特别注意电流方向和电压极性,即: 电流$i$的方向和电压$v$的极性必须符合被动符号约定。
需要指出的是,并不是所有的电阻器都遵守欧姆定律,遵守欧姆定律的电阻称为线性电阻。线性电阻的电阻值是恒定的,因此其电流-电压特性下图 (a) 所示:其 $i-v$ 图为一条通过原点的直线。非线性电阻不遵循欧姆定律。其电阻随电流变化,其 $i-v$ 特性通常下图(b) 所示。
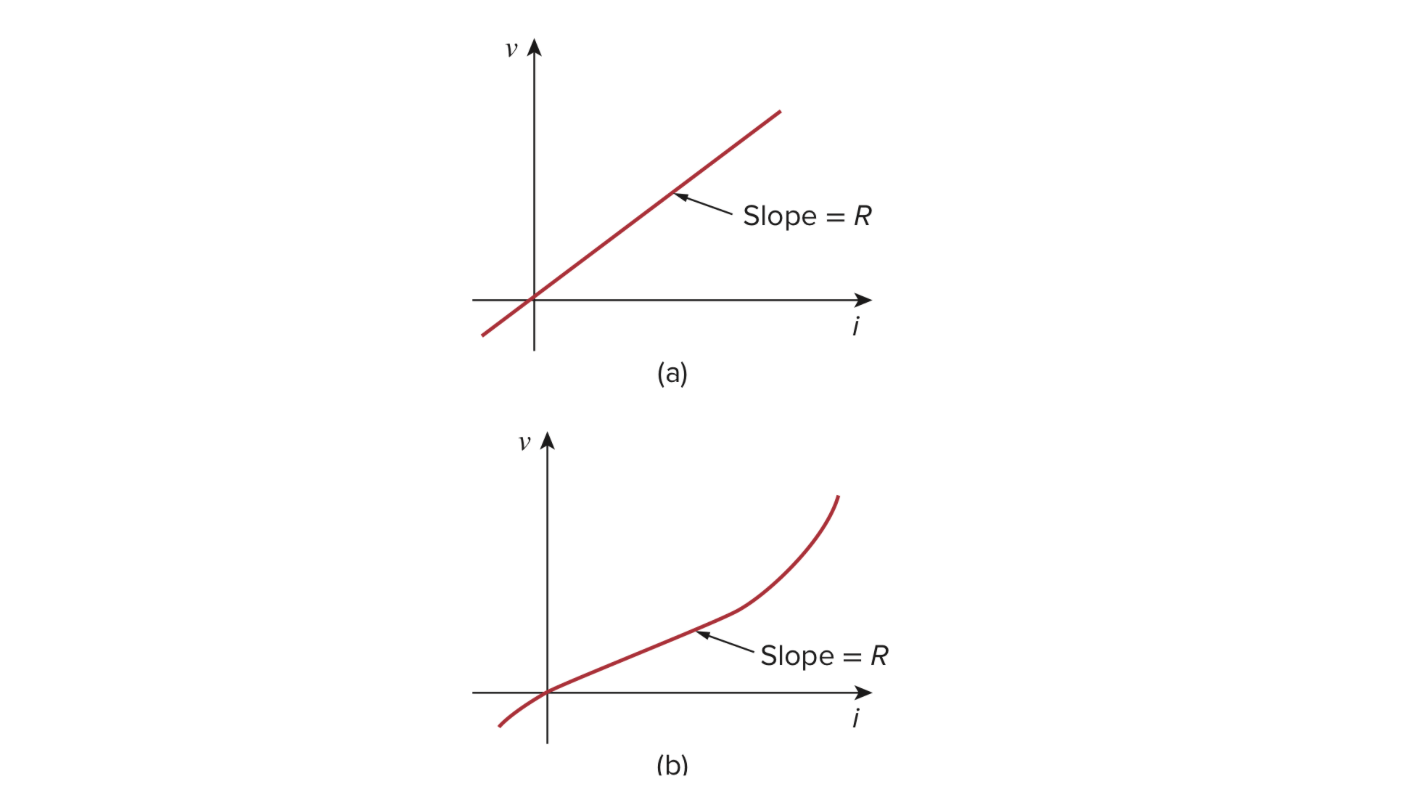
2、基尔霍夫定律(Kirchhoff’s Laws)
介绍基尔霍夫定律需要知道节点(Nodes)、支路(Branches)、环路(Loops)的定义。基尔霍夫定律可进一步分为基尔霍夫定律电流定律(Kirchhoff’s Current Laws,KCL)与基尔霍夫定律电压定律(Kirchhoff’s Voltage Laws, KVL)。
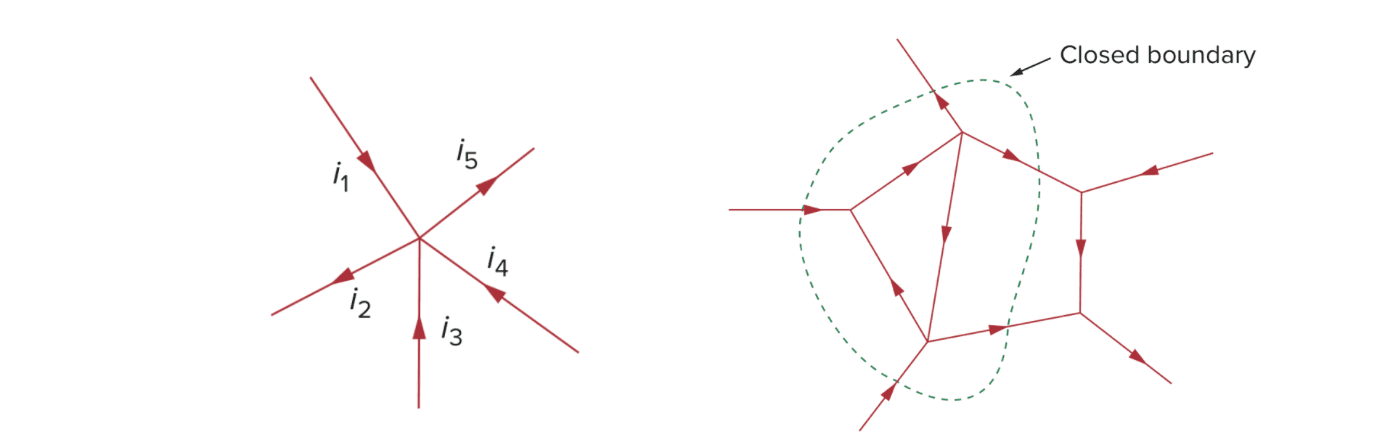
基尔霍夫电流定律 (KCL) 指出进入节点(或封闭边界)的电流的代数和为零。表示为:
$$\sum_{n=1}^{N}i_n = 0$$
其中 $N$ 是连接到该节点(或封闭边界)的分支数,$i_n$ 是第 n 个进入或离开该节(或封闭边界)点的电流。 根据该定律,进入节点的电流可以被视为正,而离开节点的电流可以被视为负。
基尔霍夫电压定律 (KVL) 指出闭合路径(或环路)环绕电压的代数和为零。表示为:
$$\sum_{m=1}^{M} v_m = 0$$
其中 $M$ 是回路中的电压数(或回路中的分支数),$v_m$ 是第 m 个电压。 每个电压上的符号是我们绕环时首先遇到分支的极性。 我们可以从任何分支开始,顺时针或逆时针绕过循环。
至此,直流电流的基本概念与基本定律介绍完毕。其它定律与方法都可以在此基础定律的基础上进行推导。因此如何使用基本定律变得非常关键。



