直流电路(5)：电容器与电感器

电容器(Capacitor)

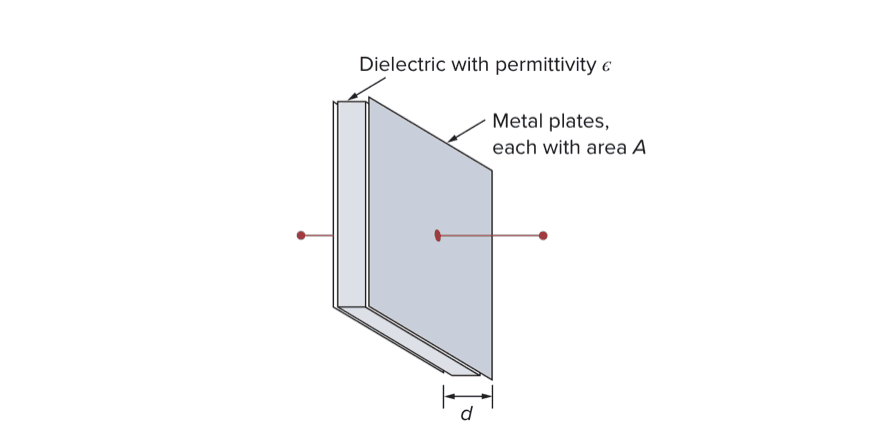
电容器是一种无源元件，可将能量存储在其电场中。 除了电阻器，电容器是最常见的电子元件。电容器由两个由绝缘体（或电介质）隔开的导电板组成。典型的电容的模型图如下：

当电压源 $v$ 连接到电容器时，电源在一个板上沉积正电荷 $q$，在另一个板上沉积负电荷 $-q$。 因此电容器存储了电荷，并且存储的电荷量（由 $q$ 表示）与施加的电压 $v$ 成正比：

$$q = Cv$$

其中，比例常数 $C$ 称为电容器的电容，单位是法拉(F, farad)。

1 farad = 1 coulomb/volt

尽管电容器的电容 $C$ 是每个极板的电荷 $q$ 与施加的电压 $v$ 之比，但它并不取决于 $q$ 或 $v$。 这取决于电容器的物理尺寸。 例如，对于平行板电容器，电容由下式给出：

$$C = \frac{\epsilon A}{d}$$

其中 $A$ 是每个板的表面积，$d$ 是板之间的距离，$\epsilon$ 是板之间介电材料的介电常数。

为得到电容的电流-电压关系，我们对$q = Cv$两边求导：

$$i = \frac{\delta q}{\delta t} = C \frac{\delta v}{\delta t}$$

电容器的电压-电流关系可以通过对$i = C \frac{\delta v}{\delta t}$进行积分得到:

$$v(t) = \frac{1}{C} \int_{t_0}^{t} i(\tau) \delta \tau + v(t_0)$$

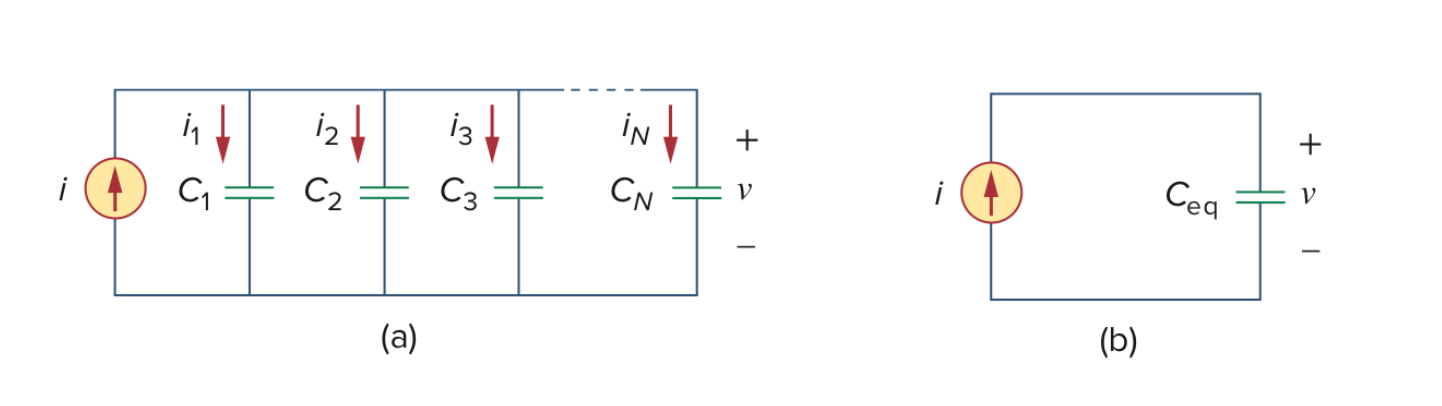
电容器的并联与串联

N个并联电容器的等效电容$C_{eq}$是单个电容的总和：

$$C_{eq} = C_1 + C_2 + C_3 + \cdots + C_N$$

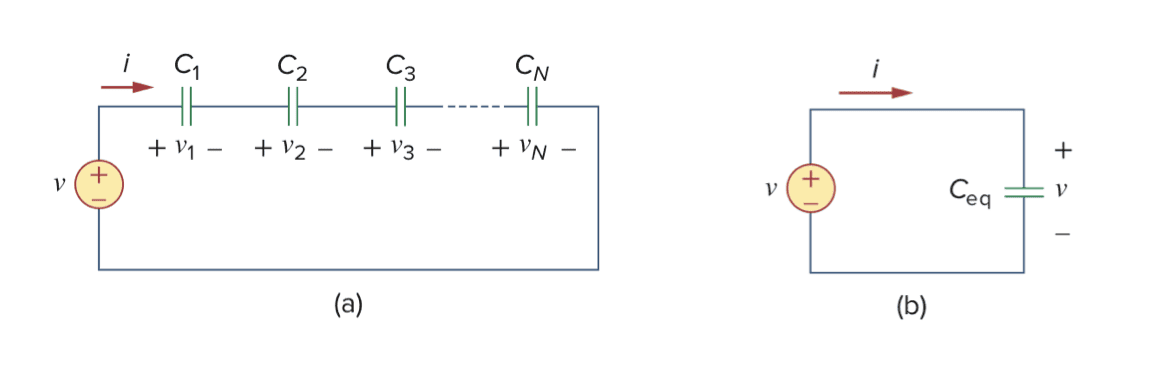
串联电容器的等效电容是各个电容的倒数之和的倒数：

$$\frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \cdots + \frac{1}{C_N} $$

电感器(Inductor)