直流电路(3)：分析定理
基尔霍夫电流与电压定律的主要优点是我们可以在不篡改其原始配置的情况下分析电路。 这种方法的一个主要缺点是，对于大型、复杂的线性电路，涉及的计算非常繁琐。因此工程师推导了线性电路下的一些定理。
为了处理复杂性，工程师们在基尔霍夫定律的基础上开发了一些定理来简化电路分析。 这些定理包括戴维宁定理(Thevenin’s theorems)和诺顿定理(Norton’s theorems)。 由于这些定理适用于线性电路，我们首先讨论线性特性。
线性特性(Linearity Property)
线性特性指的是输入与输出之间的线性关系，具体为缩放性(Scaling)和叠加性(Additivity)。 尽管该性质适用于许多电路元件，但在本章中只讨论电阻元件。
缩放性：如果输入乘以一个常数，那么输出也乘以相同的常数。对于：
$$v = iR$$
如果输入电流$i$乘以$k$，则输入电压$v$也乘以$k$
$$kiR = kv$$
叠加性：输入总和的响应是每个输入响应的总和。对于：
$$v_1 = i_1 R$$
$$v_2 = i_2 R$$
对于输入电流($i_1 + i_2$)，输出电压为：
$$v = (i_1 + i_2)R = v_1 + v_2$$
叠加原理(Superposition)
如果一个电路有两个或多个独立的电源，确定特定变量（电压或电流）值的一种方法是使用电路分析方法（节点或网格分析法）。另一种方法是确定每个独立源对变量的贡献，然后将它们相加。后一种方法被称为叠加原理。
应用叠加原理需要注意两个方面：
- 分析一个独立源时需要而关闭其他独立源，即是将每个电压源替换为0V（或短路），将每个电流源替换为0A（或开路）。通过这种方式可获得了一个更简单、更易于管理的电路。
- 非独立电源保持不变，因为它们由电路变量控制。
电源变换(Source Transformation)
戴维南定理(Thevenin’s Theorem)
戴维南定理指出：线性两端电路可以由电压源 $V_{Th}$ 与电阻 $R_{Th}$ 串联组成的等效电路代替，其中$V_{Th}$ 是开路端子处的电路电压，$R_{Th}$ 是独立电源关闭时端子处的输入或等效电阻。
如果计算戴维南等效电压$V_{Th}$ 与电阻$R_{Th}$？假如下图两个电路等效，那么两个电路在ab两端具有相同的电压-电流关系(v-i relation)。
1、计算戴维南等效电压$V_{Th}$
移除ab两端的负载，使ab两端保持开路状态，戴维南等效电压$V_{Th}$ 就是ab两端的开路电压。$V_{Th}$可以通过计算得到，也可以通过直接测量(下图a)。
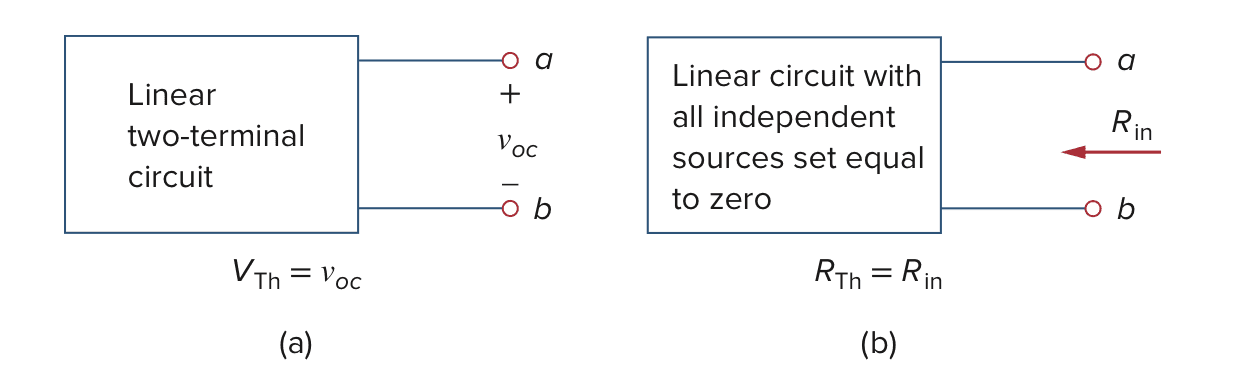
2、计算戴维南等效电阻 $R_{Th}$
移除ab两端的负载，使ab两端保持开路状态，戴维南等效电阻 $R_{Th}$就是独立电源为0时的电阻。$R_{Th}$可以通过计算得到(上图b)，也可以通过测量得到，即将ab两端短路并测量两端电流$i$，然后通过以下公式计算：
$$R_{Th} = \frac{v_{Th}}{i}$$
