直流电路(2)：分析方法

基于电路理论的基本定律(欧姆定律和基尔霍夫定律)，我们可以推导出两种强大的电路分析方法：采用基尔霍夫电流定律的系统应用的节点分析(Nodal Analysis)，与采用基尔霍夫电流定律的网格分析(Mesh Analysis)。利用这两种方法，我们可以通过联立方程来分析任何线性电路，然后求解这些方程以获得所需的电流或电压值，而且可以借用Matlab, Pspice等分析软件。

本章的分析方法通常需要使用计算机，因此了解下基本概念便可以。

节点分析方法

节点分析方法基于节点的基尔霍夫电流定律。

1、不考虑电压源

简化起见，先不考虑有电压源的电路，节点分析方法的大体步骤如下：

1. 选择一个节点作为参考节点。 分配电势 $v_1$, $v_2,$ . . . , $v_{n − 1}$到剩余的$n − 1$个节点。 各个节点电压相对于参考节点。
2. 将基尔霍夫电流定律应用于$n-1$个非参考节点中的每一个。 使用欧姆定律以节点电压表示支路电流。
3. 求解生成的联立方程以获得未知节点电势。

通过一个案例理解以上分析步骤：

案例1

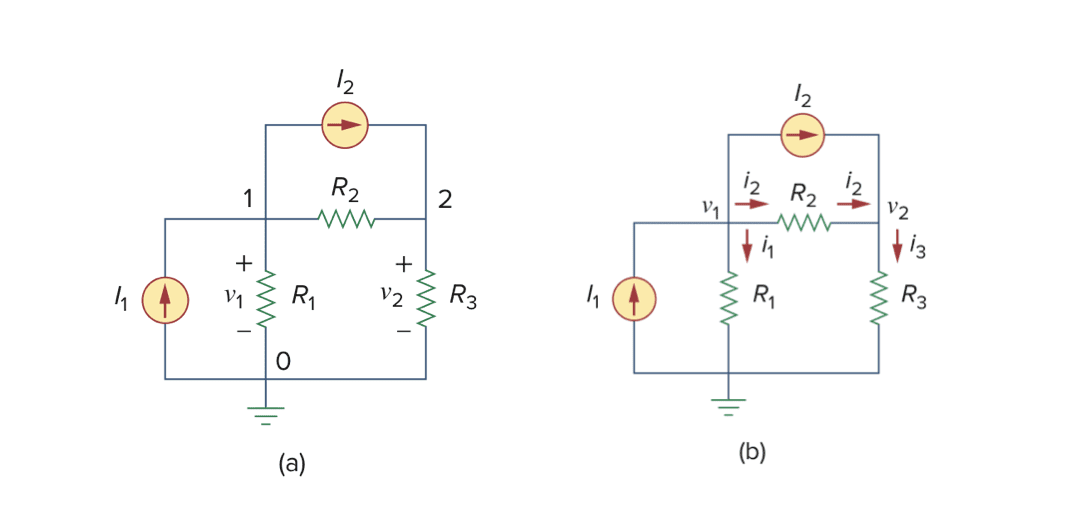
第一步：图(a)选择节点0点作为参考点，参考节点的电势为零。节点1与节点2分别分配电势$v_1$与$v_2$。务必要记住$v_1$与$v_2$是相对参考节点0.

第二步：为了更清楚地表示节点的电势与电流，把图(a)简化成图(b)，另外将基尔霍夫电流定律应用于节点1与节点2，得到：

节点1: $I_1 = I_2 + i_1 + i_2$

节点2: $I_2 + i_2 = i_3$

然后通过欧姆定律用电压来替代电流，得到：

节点1: $I_1 = I_2 + \frac{v_1}{R_1} + \frac{v_1 - v_2}{R_2}$

节点2: $I_2 + \frac{v_1 - v_2}{R_2} = \frac{v_2}{R_3}$

第三步：解第二步得到的联合方程组。

2、考虑电压源

若是考虑电压源，节点分析有两种情况：

1. 如果电压源连接在参考节点和非参考节点之间，我们只需将非参考节点处的电压设置为等于电压源的电压。
2. 如果电压源连接在两个非参考节点之间，则这两个非参考节点形成一个广义节点或超节点(Supernode)； 我们应用基尔霍夫电流定律(KCL) 和基尔霍夫电压定律(KVL )来确定节点电压。

网格分析方法

网格分析方法基于节点的基尔霍夫电压定律。

环路是一条闭合路径，没有节点经过超过一次。网格是其中不包含任何其他环路的环路。网格分析应用 KVL 来查找未知电流，这个分析方法不像节点分析那么通用，因为它仅适用于平面电路。平面电路是可以在平面上绘制且没有分支相互交叉的电路。

工程应用大部分是通过计算机来计算，所以这里不进一步介绍理论，大家只需要知道有这个概念。