直流电路(4)：运算放大器

基础概念

运算放大器(Operational Amplifiers, op amp)是一种有源电路元件，设计用于执行加法、减法、乘法、除法、微分和积分的数学运算。运算放大器在商业上以多种形式以集成电路封装形式提供。下图显示了一个典型的八引脚双列直插式封装(dual in­line package, DIP)。

运算放大器有5个重要的引脚：

1. 反相输入端(Inverting input)，引脚2。
2. 同相输入端(Noninverting input)，引脚3。
3. 输出端(output)，引脚6。
4. 正极电源端$V^+$，引脚7。
5. 负极电源端$V^-$，引脚4。

引脚8没有使用，引脚1与5很少使用。

同相输入端的输入信号，输出端输出相同的极性出现；反相输入端的输入信息，输出端输出相反的极性。

作为有源元件，运算放大器必须由电压源供电(左下图)。 尽管为了简单起见，运算放大器的电路图经常忽略电源，但不能忽略电流。电流遵守基尔霍夫电流定律：

$$i_0 = i_1 + i_2  + i_+ + i_-$$

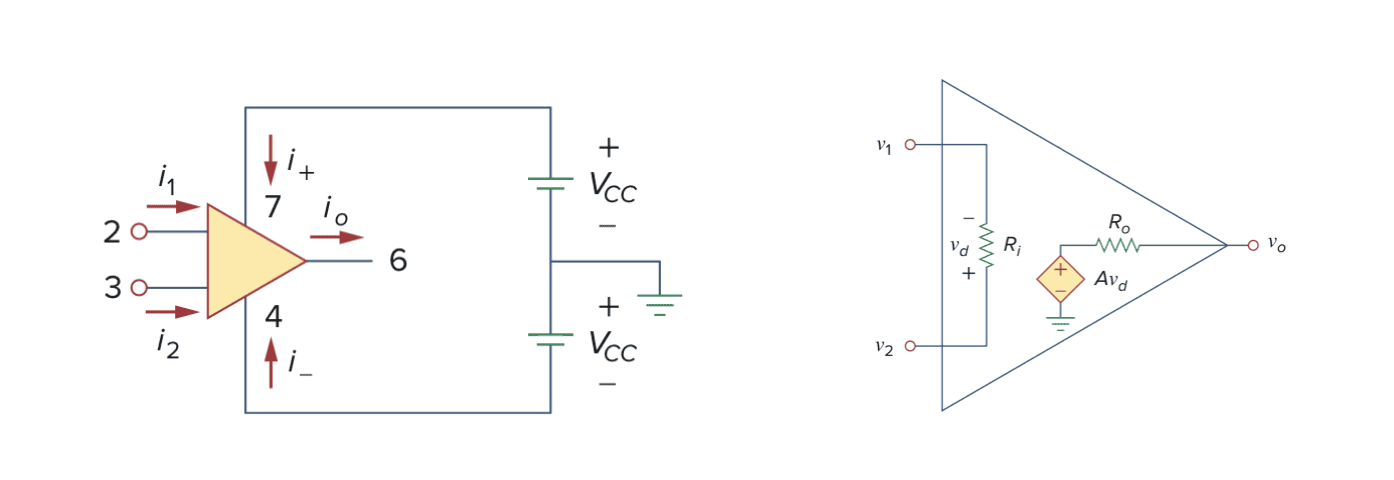
右上图为非理想运算放大器的电路简化图。 输出部分由电压控制源$Av_d$与串联的输出电阻 $R_0$ 组成， 输入部分由电阻 $R_i$ 组成。其中输入电极$R_i$ 与输出电阻 $R_o$ 是戴维南等效电阻。 差分输入电压 $v_d$ 由下式给出：

$$v_d = v_2 - v_1$$

其中 $v_1$ 是反相端与地之间的电压，$v_2$ 是同相端与地之间的电压。

运算放大器感测两个输入之间的差异，将其乘以增益 $A$，并导致产生的电压出现在输出端。因此输出电势$v_0$为：

$$v_0 = Av_d = A(v_2 - v_1)$$

$A$ 称为开环电压增益(Open-loop voltage gain)，即输出到输入之间没有反馈情况下运算放大器的增益。下图显示了电压增益 $A$、输入电阻 $R_i$、输出电阻 $R_o$ 和电源电压 $V_{CC}$ 的典型值。

反馈(Feedback)的概念对于我们理解运算放大器电路至关重要。 当输出反馈到运算放大器的反相端时，就实现了负反馈。当从输出到输入存在反馈路径时，输出电压与输入电压之比称为闭环增益(Closed-loop gain)。运算放大器的限制是其输出电压的幅度不能超过 $|V_{CC}|$。 换句话说，输出电压取决于电源电压并受其限制。

理想运算放大器

理想的运算放大器是具有无限开环增益、无限输入电阻和零输出电阻的放大器。

1. 无限开环增益 $A \cong \infty$
2. 无限输入电阻$R_i \cong \infty$
3. 零输出电阻R_o = 0$

虽然理想运算放大器仅提供近似的分析，但运算放大器具有很大的增益和输入阻抗，因此近似分析是一个非常实用的方法，而且与实际相差不远。 理想运算放大器的模型图如下：

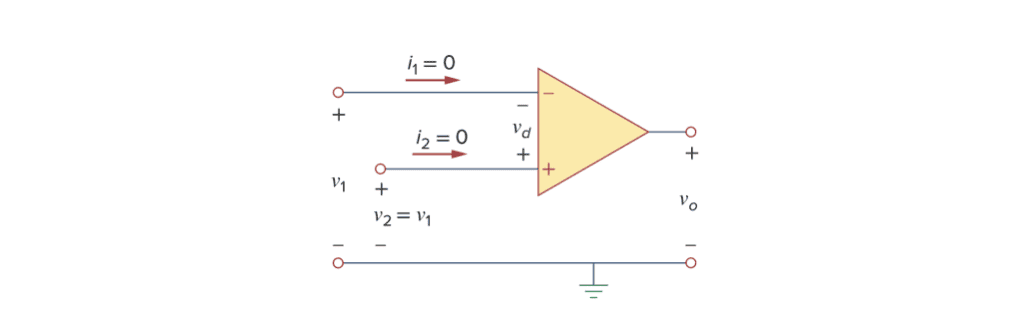
理想运算放大器的两个重要特性是：

1. 流入两个输入端子的电流为零。 这是由于无穷大的输入电阻，输入端子之间相当于在开路，电流无法进入运算放大器，即$i_1 = i_2 = 0$。 但输出电流不一定为零。
2. 输入端子两端的电压为零，即$v_d = v_2 - v_1$，或者$v_1 = v_2$。