交流电路(1):正弦交流电和相量
正弦电流通常称为交流电(Alternating Current, AC),具有交替的正值和负值。 由正弦电流更容易生产与传输,在生活在广泛使用。

正弦交流电(Sinusoids)
正弦交流电是具有正弦或余弦函数形式的信号,用余弦来表示:
$$v(t) = V_m \sin(\omega t + \phi)$$
- $V_m$ = 正弦交流电的振幅出
- $\omega$ = 角频率,单位为弧度/秒
- $\phi$ = 正弦交流电的相位
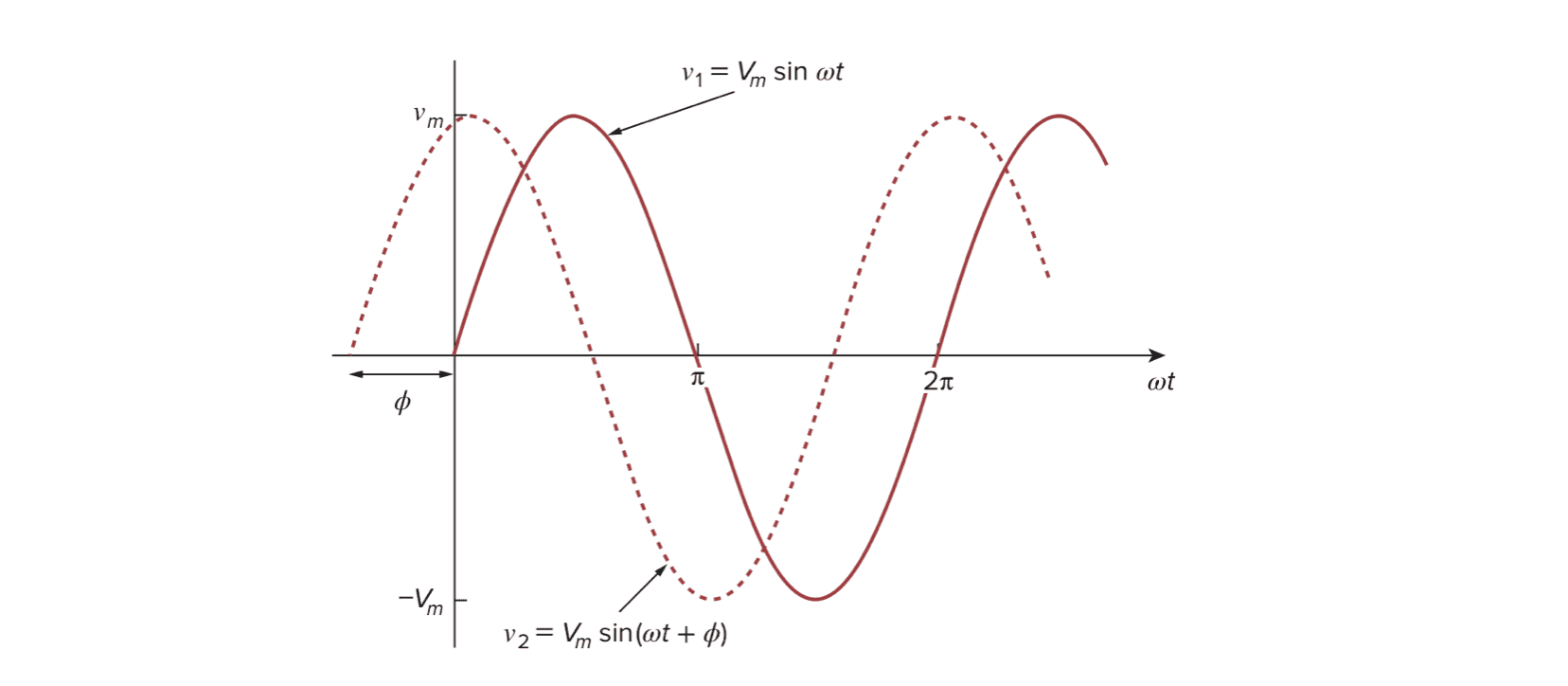
对于两个交流电$v_1(t) = V_m \sin(\omega t)$与$v_2(t) = V_m \sin(\omega t + \phi)$,$v_2(t)$图像相对于$v_1(t)$图像整体左移了$\phi$,我们称之为$v_2(t)$相位超前$\phi$,或者$v_1(t)$相位滞后$\phi$。
相量(Phasor)
正弦曲线很容易用相量表示,相量比正弦与余弦函数更方便使用。
1、复数与相量
在定义相量并将其应用于电路分析之前,我们需要彻底熟悉复数:
$$z = x + jy$$
其中$j = \sqrt{-1}$。复数有三种形式:
- 矩形形式(Rectangular form):$z = x + jy$
- 极坐标形式(Polar form):$z = r \angle \phi$
- 指数形式(Exponential form):$z = r e^{j \phi}$
相量(Phasor)表示法的基础是欧拉恒公式 :
$$e^{j\phi} = \cos \phi + j \sin \phi$$
- $\cos \phi$是$e^{j\phi}$的实部:$\cos \phi = Re(e^{j\phi})$
- $\sin \phi$是$e^{j\phi}$的虚部:$\sin \phi = Im(e^{j\phi})$
对于正弦曲线 $v(t) = V_m cos(\omega t + \phi)$,用欧拉表达式来表示为:
$$v(t) = V_m cos(\omega t + \phi) = Re(V_m e^{j(\omega t + \phi)}) = Re(V_m e^{j \phi} e^{j\omega t}) = Re(\textbf{V} e^{j\omega t})$$
其中$\textbf{V}$为相量(Phasor):
$$\textbf{V} = V_m e^{j \phi} = V_m \angle \phi$$
相量$\textbf{V}$表示了正弦交流电的幅度和相位的复数。 虽然相量中没有体现频率,在处理相量时,务必牢记相量的频率 ω; 否则我们会犯严重的错误。
2、正弦波与相量
如果要得到相量 $\textbf{V}$对应的正弦波,需要将相量乘以时间因子 $e^{j \omega t}$ 并取复数的实部。
$$\textbf{V} = V_m e^{j \phi} $$
$$v(t) = Re(\textbf{V} e^{j \omega t}) = Re(V_m e^{j \phi} e^{j \omega t} ) = V_m cos(\omega t + \phi)$$
如果要得到正弦波对应的相量,需要将正弦波表示为余弦形式,这样正弦波就可以写成复数的实部。 然后我们剔除时间因子$e^{j\omega t}$,剩下的就是正弦曲线对应的相量。通过剔除时间因素,我们将正弦波从时域变换到相量域。
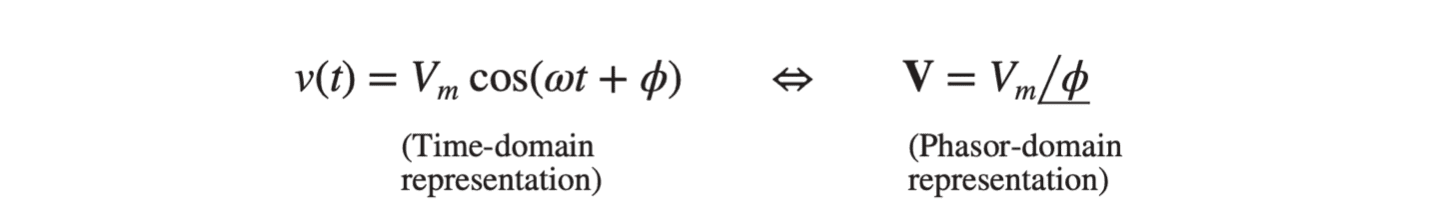
总结
正弦波$v(t) = V_m cos(\omega t + \phi$可通相量$textbf{V} = V_m e^{j \phi}$来表示,但两者不是等号关系。相量需要乘以时间因子 $e^{j \omega t}$ ,然后取实部才是正弦波。
为什么要使用相量?
因为交流电中频率通过是固定的,使用相量可以简化有电容、电感等微分积分电路的计算,从而不用去求解复杂的微分或者积分方程。
电路元件的相量关系
我们知道如何在相量域中表示电压或电流,但如何将其应用于无源元件 R、L 和 C 的电路?接下来将每个元件的电压-电流关系从时域转换到相量域。
1、电阻器R
如果通过电阻器R的电流为: $i = I_m \cos(\omega t + \phi)$
则电容器两端的电压为:$v = iR = RI_m \cos(\omega t + \phi)$
电压相量为:$\textbf{V} = RI_m \angle \phi$
电流相量为:$\textbf{I} = I_m \angle \phi$
最后得到:
$$\frac{\textbf{V}}{\textbf{I}} = R$$
2、电容器C
如果通过电容的电压为: $v(t) = V_m \cos(\omega t + \phi)$
则电容器两端的电流为:$i = C \frac{\delta v}{\delta t} = \omega C V_m \cos(\omega t + \phi + 90^{\degree})$
电压相量为:$\textbf{V} = V_m \angle \phi$
电流相量为:$\textbf{I} = \omega C V_m \angle \phi + 90^{\degree}$
最后得到:
$$\frac{\textbf{V}}{\textbf{I}} = \frac{1}{j\omega C}$$
3、电感器L
如果通过电感器L的电流为: $i = I_m \cos(\omega t + \phi)$
则电容器两端的电压为:$v = L \frac{\delta i}{\delta t} = \omega L I_m \cos(\omega t + \phi + 90^{\degree})$
电压相量为:$\textbf{V} = \omega L I_m \angle \phi + 90^{\degree}$
电流相量为:$\textbf{I} = I_m \angle \phi$
最后得到:
$$\frac{\textbf{V}}{\textbf{I}}= j\omega L$$
下表列出了时间域、相量域的电流-电流关系。

阻抗与导纳(Impedance and Admittance)
我们推导了R、C、L三个元件在相量域中电压-电流的关系:
$$\frac{\textbf{V}}{\textbf{I}} = R \ , \frac{\textbf{V}}{\textbf{I}} = \frac{1}{j\omega C} \ , \frac{\textbf{V}}{\textbf{I}} = j\omega L$$
根据三个表达式,我们定义了欧姆定律的相量形式:
$$ \textbf{Z} = \frac{\textbf{V}}{\textbf{I}}$$
其中\textbf{Z}是一个与频率相关的量,称为阻抗,以欧姆为单位测量。阻抗表示电路对正弦电流流动的反抗。 虽然阻抗是两个相量的比值,但是它不是相量,因为它不对应一个正弦变化的量。
相量域的基尔霍夫定律
直流电路基础中有介绍基尔霍夫定律(Kirchhoff’s Laws)。在交流电的情况下,基尔霍夫定律对于相量(Phasors)同样适用。
对于环路的KVL:
$$\textbf{V}_1 + \textbf{V}_2 + \cdots + \textbf{V}_n = 0$$
对于节点的KCL:
$$\textbf{I}_1 + \textbf{I}_2 + \cdots + \textbf{I}_n = 0$$
阻抗串联与并联
阻抗串联与并联与直流电路的电阻串联与并联一样。
对于串联电路:
$$\textbf{Z}_{eq} = \textbf{Z}_1 + \textbf{Z}_2 + \cdots + \textbf{Z}_N$$
对于并联电路:
$$\frac{1}{\textbf{Z}_{eq} } = \frac{1}{\textbf{Z}_1} + \frac{1}{\textbf{Z}_2 } + \cdots \frac{1}{\textbf{Z}_N}$$



